Functions And Its Types in Mathematics With Examples

Functions :

➤ A function is an equation for which any x that can be put into the equation will produce exactly one output such as y out of the equation.

➤ It defines a relationship between one variable (the independent variable) and another variable (the dependent variable).

➤ It is represented as,

y = f(x)

,where x is an independent variable and y is a dependent variable.

➤ For example: y = 18x + 7.

Inverse Function

The inverse of a function is the type of function in which the domain and range of the given function is reverted as the range and domain of the inverse function.

The inverse function f(x) is denoted by f^-1(x).

Rational Function

A rational function is any function which can be represented by a rational fraction say, f(x)/g(x) in which numerator, f(x) and denominator, g(x) are polynomial functions of x, where g(x) ≠ 0.

Quadratic Function

All functions in the form of y = ax² + bx + c where a, b, c ∈ R, a ≠ 0 will be known as Quadratic functions. The graph will be parabolic.

Cubic Function

A cubic polynomial function is a polynomial of degree three and can be expressed as:

F(x) = ax³ + bx² + cx + d, and a is not equal to zero.

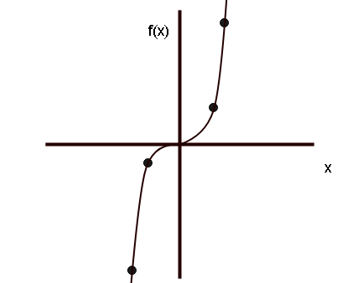
Polynomial Function

A Polynomial function is a sort of function that can be represented as a polynomial. It is expressed as,

f(x) = a₀ + a₁x + a₂x² + … + a_nxⁿ
,where n represents a non-negative integer and a₀, a₁, a₂, …, a_n∈R.
For example, f(x)=3x+7 is a polynomial function.

Modulus Function

The function f(x) = |x| is called a modulus function.

The modulus function returns the absolute value of the given function, irrespective of the sign of the input domain content.

Constant Function

If the function f: R→R is defined as f(x) = y = c, for x ∈ R and c is a constant in R, then such function is known as Constant function. The domain of the function f is R and its range is a constant, c.

One-to-One Functions

A function in which one element of Domain Set is connected to one element of Co-Domain Set.

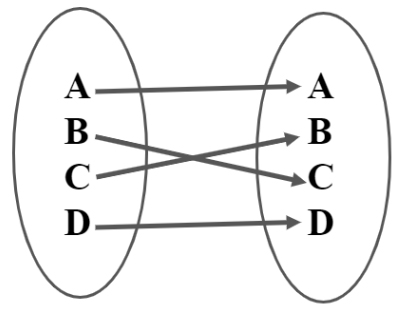
Onto Functions

In the case of an onto function, every element in the codomain is related to the domain element. For a function defined by f: A → B, such that every element in set B must have a pre-image in set A.

One-to-One Onto Functions

A function which is both one to – one and onto is called One-to-One Onto Function.

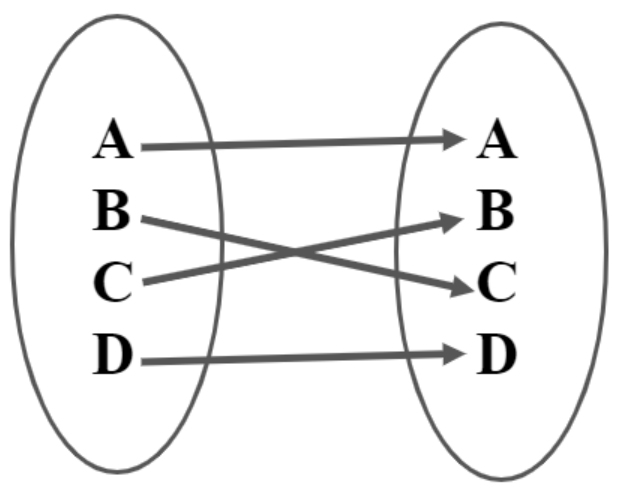
Into Functions

A function in which there must be an element of co-domain Y does not have a pre-image in domain X.

One-One Into Functions

Let f: X → Y. The function f is called one-one into function if different elements of X have different unique images of Y.

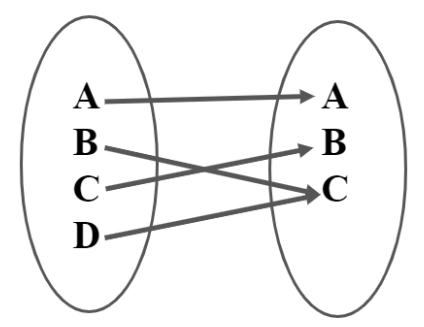
Many-One Functions

It can be defined by the function f: A → B, such that more than one element of set A is connected to the same element in set B. In this case, more than one element has the same co-domain or image.

Many-One Into Functions

Let f: X → Y. The function f is called the many-one function if and only if is both many one and into function.

Many-One Onto Functions

Let f: X → Y. The function f is called many-one onto function if and only if is both many one and onto.

Examples

1. y = 2x +7
2. f(x) = 7x + 4
3. y = 7/x
4. y = tanx
5. y = (3x – 7)/(7x + 1)