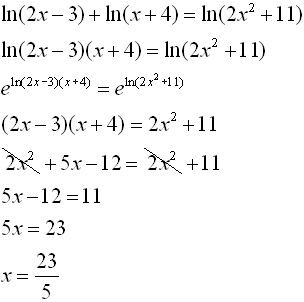Logarithmic Functions: Definition, Properties & Examples

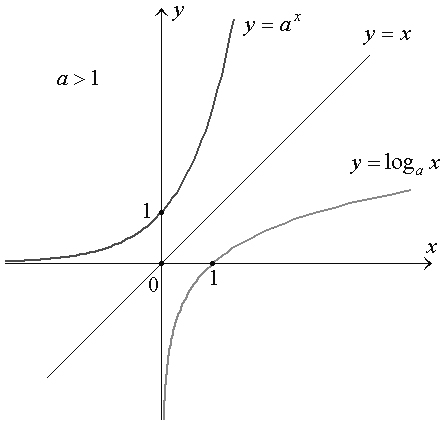
Logarithmic Functions

logarithm, the exponent or power to which a base must be raised to yield a given number.

The logarithmic function is an inverse function to exponentiation.

Expressed mathematically as. For, y= log_a x if and only if x = a^y , Where x > 0 , a > 0, and a ≠1

For example, 4³ = 64; therefore, 3 is the logarithm of 64 to base 4, or 3 = log₄ 64.

Power Rule

Raise an exponential expression to a power and multiply the exponents together.

Log_b X^y = y log_b X

Base Change Rule

If b and x are positive numbers and b ≠ 1, x ≠ 1, then;

log_b (x) = ln x / ln b or log_b (x) = log₁₀ x / log₁₀ b

Multiply Rule

Multiply two numbers with the same base, add the exponents.

log_b XY = log_b X + log_b Y

Divide Rule

Divide two numbers with the same base, subtract the exponents.

log_b X/Y = log_b X – log_b Y

Zero Exponent Rule

log value of 1 is always zero for any base b.

log_b 1 = 0

Reciprocal rule

If b and x are the positive numbers other than 1, then;

log_bx = 1/log_xb

Summation rule

log_b X + log_b Y = log_b XY

Subtraction rule

log_b X – log_b Y = log_b X/Y

Examples 1

Find log₂(1/64)

= log₂(1/64)

= log₂1 – log₂64

= log₂1 – log₂2⁶

= 0 – 6log₂2

= -6(1)

= -6

Examples 2

Find value of x for below example.