Here you will get all details about Isohyetal Method and other Various methods of calculating average rainfall over area. There are several methods to calculate average rainfall over a given area. We will discuss all methods in detail here.
Various methods of calculating average rainfall over area
There are several methods to calculate average rainfall over a given area. The choice of method often depends on the available data and the level of accuracy required. Here are a few common methods:
- Arithmetic Mean Method
- Theissen Polygon Method
- Iso-Hyetal Method
Isohyetal Method
In this method, isohyetal lines (lines connecting points of equal rainfall) are drawn on a map. The area between these lines is divided into polygons, and the average rainfall for each polygon is calculated. The overall average is then determined by weighting each polygon’s average by its area.
- This is considered as one of the most accurate methods, but it is dependent on the skill and experience of the analyst.
- The method requires the plotting of isohyets as shown in the figure and calculating the areas enclosed either between the isohyets or between an isohyet and the catchment boundary.
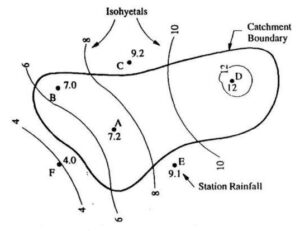
- In the isohyetal method, precipitation values are plotted at their respective stations on a suitable base map, and isohyets are drawn to create an isohyetal map. Isohyetal lines are based on interpolation between rain gauge stations. While constructing isohyets, it is assumed that rainfall between two stations varies linearly, unless abrupt changes in topography indicate otherwise.
- The areas may be measured with a planimeter if the catchment map is drawn to a scale.
- Iso-hyetal method is used for basins having area more than 5000 km2.
Isohyt
It is a line joining points of equal rainfall for a given interval. Isohyets are contours of equal precipitation analogous to contour lines on a topographic map.
Properties of Iso-hyetes
- Two different iso-hyetes do not cross each other;
- Iso-hyet of higher value shows the places which receive more rainfall;
- Each iso-hyet must close on itself or must go out of the area under consideration.
Advantages of Isohyetal Method
The Isohyetal Method for calculating average rainfall has several advantages, making it a valuable approach in certain situations. Here are some of the advantages:
1. Spatial Distribution:
- The Isohyetal Method provides a spatial distribution of rainfall by identifying lines of equal precipitation (isohyets). This allows for a more detailed understanding of how rainfall varies across the area, which is crucial for applications such as hydrology and agriculture.
2. Localized Variability:
- It accounts for the localized variability of rainfall patterns within a given area. This is particularly important in regions with complex topography, where rainfall can vary significantly over short distances.
3. Topographical Considerations:
- The method takes into consideration the influence of topography on rainfall. Areas with different elevations may experience different amounts of precipitation, and the Isohyetal Method helps capture this variation.
4. Visualization:
- The resulting isohyetal map is a visual representation of rainfall distribution, making it easy to interpret and communicate to various stakeholders, including researchers, policymakers, and the general public.
5. Integration with GIS:
- Geographic Information System (GIS) tools can be used to implement the Isohyetal Method effectively. This integration allows for the analysis of spatial patterns, and GIS can assist in creating accurate isohyetal maps.
6. Flexibility:
- The Isohyetal Method is flexible and can be adapted to different scales, from small watersheds to large regions. This adaptability makes it suitable for various applications, including water resource management, land-use planning, and environmental impact assessments.
7. Quantitative Data:
- The method provides quantitative data on average rainfall for specific areas, making it useful for numerical analysis and modeling. This information is valuable in fields such as hydrology, where precise rainfall data is crucial.
8. Integration with Hydrological Models:
- Isohyetal maps can be used as input data for hydrological models, enhancing the accuracy of modeling studies that require spatially distributed rainfall information.
9. Historical Analysis:
- Isohyetal maps can be created for different time periods, allowing for historical analysis of rainfall patterns and trends. This is valuable for understanding long-term climatic variations and trends.
While the Isohyetal Method offers these advantages, it’s essential to note that the accuracy of the results depends on the quality and density of the rainfall data, as well as the appropriateness of the interpolation techniques used to generate isohyetal lines. Additionally, for very large areas, the method may become less practical due to the challenge of collecting sufficient data.
Dis-Advantages of Isohyetal Method
While the Isohyetal Method has several advantages, it also comes with certain disadvantages and limitations. It’s important to consider these factors when choosing a method for calculating average rainfall over an area:
1. Data Requirements:
- The Isohyetal Method heavily relies on accurate and dense rainfall data from various locations within the study area. In regions with limited or sparse rain gauge coverage, the method may produce less reliable results.
2. Spatial Variability:
- Isohyetal maps assume a uniform distribution of rainfall within each isohyetal contour. In reality, rainfall can vary significantly within these contours, especially in areas with complex topography, land cover, or local weather patterns.
3. Interpolation Errors:
- The method involves interpolation between observed points to create isohyetal lines. Interpolation introduces errors, and the accuracy of the results depends on the chosen interpolation technique. Different interpolation methods may produce varying results.
4. Scale Dependency:
- The accuracy of the Isohyetal Method is often scale-dependent. As the size of the study area increases, the assumption of spatial uniformity becomes less accurate. This limits the method’s applicability for large-scale regional assessments.
5. Temporal Variability:
- Isohyetal maps provide a snapshot of average rainfall for a specific time period. They may not capture temporal variations, such as seasonal patterns, long-term trends, or extreme weather events, which can be important for certain applications.
6. Subjectivity in Line Drawing:
- Drawing isohyetal lines is a subjective process and can be influenced by the mapmaker’s judgment. Different mapmakers may draw isohyets differently, leading to potential inconsistencies and biases in the results.
7. Limited Physical Interpretation:
- While Isohyetal maps provide a visual representation of rainfall distribution, they may lack a direct physical interpretation of the underlying meteorological processes that influence rainfall variability in the area.
8. Sensitivity to Outliers:
- The Isohyetal Method can be sensitive to outliers or extreme values from individual rain gauge stations. A single station with an exceptionally high or low rainfall measurement can disproportionately influence the results.
9. Inability to Capture Small-Scale Variability:
- Isohyetal maps may not effectively capture small-scale variations in rainfall, especially in areas with microclimates or localized weather phenomena. This limitation is particularly relevant for applications requiring high-resolution spatial information.
10. Challenges in Heterogeneous Terrain:
- In regions with complex topography or heterogeneous land cover, the Isohyetal Method may struggle to accurately represent the spatial distribution of rainfall. Terrain features can lead to significant variations in precipitation that the method might not fully capture.
When using the Isohyetal Method, it’s essential to carefully consider these limitations and, if possible, complement the analysis with other methods or data sources to enhance the accuracy and reliability of the results.
Arithmetic Mean Method
The arithmetic mean is the most straightforward method. It involves adding up the total rainfall for a specified period and dividing it by the number of data points (locations or time periods).
Theissen Polygon Method
This method involves creating polygons around each rain gauge station and assigning each polygon to the nearest station. The rainfall data from each station is then multiplied by the area of its corresponding polygon. The average is calculated by summing these values and dividing by the total area.
Download Our App
“Vlcinfo” is an Educational App where you will be able to find details about various Job Related Updates, Test Series, Results, Syllabus, Old Papers, Video Lectures, MCQs Practice and much more.

App Features :
- Job Related Updates
- Test Series
- Video Lectures
- Study Materials
- Current Affairs
- Old Papers
- MCQs Practice